Modelling Adversarial Communication using DNNs

Updated on •

categories - machine_learning

tags - cryptography, deep neural networks tensorflow


This midsems, my Cryptosystem teacher advised to either take exams seriously or to make a project. Well, the exams never bothered me anyway :p (and because of that I don't score good in them), but I really thought of making something for project that would also help me improve my understanding of deep neural nets. So after researching, I found a good paper published by Google Brain Team, the link is in description, which had some proofs that a network can learn to protect information from adversaries. So I decided to implement model they presented. This would make a good networking project and I would also produce visualizations from TensorBoard, that I needed for this blog post.

TLDR (for research paper)
The famous old example for Alice, Bob, and Eve is used in the discussion. Check the model -
Alice, Bob, and Eve, with a symmetric cryptosystem.
There are convnets, and fully-connected layers implemented for all three, but the basic difference is of the key. It can be viewed as a generative adversarial neural network (according to wikipedia, these are the ones, that train while competing), having two optimizers, which oppose each other, but with single network. As all other parameters are the same for the optimizers, the difference lies in the network itself, which is the key is not provided with the input at the Eve node. The optimizer which has the key outperforms the one without, and hence results in large error bits on the Eve node.

Results
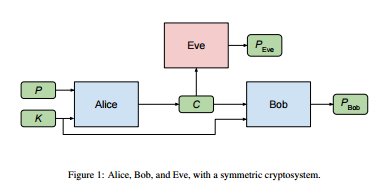
Well, I didn't go onto the scale the paper suggests (limitation of resources), but the visualizations here are pretty promising that the network is learning. Below are the error bit rates. I believe if trained long enough, the model would approach 0 bits for bob, and almost 8 bits for eve as said in the paper, although here too, the relation can be seen distinctively, with 2 and 11 bits respectively. The visualizations are created using TensorBoard, as told in this post.

Wrong bits that Bob predicted. Almost 2 bits.
Wrong bits that Eve predicted. Almost 11 bits.

Links

  1. Google Brain Paper
  2. Github Repo