Glove - Word Vectors
Updated on
•
by - pranav
categories - the_mathetics_behind
Word vectors are the basic building of NLP tasks for deep learning. Neural nets are trained using matrix calculations. And matrix consists of numbers. So to train the network we need to represent the words in our corpus into numerical row vectors so that we can feed them to our network for learning. Several methods have been tried for this problem, I would list them
- SVD Based Methods
- Word Document Matrix
- Window based Co-occurence Matrix
- SVD on Co-occurence Matrix
- Neural Network Models
- Word2Vec
- Glove
Co-occurence Matrix : $X$
Co-occurence count of word (i,j) : $X_{ij}$
Count/Frequency of word i : $\sum{}_{j}X_{ij}$
Probability of word j occuring with word i : $X_{ij}/X_{i}$
Conditional Probability : $P(k|w) = P_{kw}/P_{w}$
Let's consider i = dog, j = cat, k = bark. If we train our model, we would see that the ratio $P_{ik}/P_{jk}$ is much higher than 1. Similarily we can see the words as depicted in the diagram. The measure of probability ratios is indicating which words are more likely to occur.
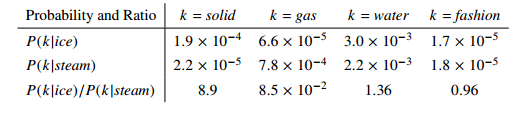
$F(w_{i}, w_{j}, w^{'}_{k}) = \dfrac{P_{ik}}{P_{jk}}$
$F(w_{i} - w_{j}, w_{k}^{'}) = \dfrac{P_{ik}}{P_{jk}}$
$F((w_{i} - w_{j})^{T}w^{'}_{k}) = \dfrac{P_{ik}}{P_{jk}}$
$\begin{align}F((w_i^T-w_j^T)\cdot w_k') & =F(w_i^T\cdot w_k'-w_j^T\cdot w_k')=F(w_i^T\cdot w_k'+(-w_j^T\cdot w_k'))\\ & =F(w_i^T\cdot w_k')\times F(-w_j^T\cdot w_k') = F(w_i^T\cdot w_k')\times F(w_j^T\cdot w_k')^{-1}\\ & = \dfrac{F(w_{i}^{T}w_{k}^{'})}{F(w_{j}^{T}w_{k}^{'})},\end{align}$
From the property of group homomorphism that it preserves inverses, we know that + has an inverse as -, so x(multiplication) would have its equivalent inverse as / (division). For finding the solution of this equation, we need to equate the rhs with the original equations,
$F(w_{i}^{T}w_{k}^{'}) = P_{ik} = \dfrac{X_{ik}}{X_{i}}$
The solution to the above equations would be F = Exp. (Exponent function). Hence,
$w_{i}w_{k}^{'} = log(P_{ik}) = log(X_{ik}) - log(X_{i})$
This equation would be symmetric if the term $X_{i}$ would be absent, or what we can do is add $X_{k}$ so that the symmetry can be acheived. Thus the equation becomes -
$w_{i}^{T}w_{k}^{'} + b_{i} + b_{k}^{'} = log(X_{ik})$
The above equation can be used for our loss function to train the word, and context vectors. We define the loss function as -
$J = \sum{}_{i,j=1}^{|V|} f(X_{ij}).(w_{i}^{T}w_{j}^{'} + b_{i} + b_{j}^{'} - log(X_{ij}))^{2}$
The function f is weight function which can be understood more in the paper itself. Basically it is a parameter that although tackles small cooccurences by not making them over-weighted, and also for the large values to prevent them from overweigting too.
$f(x) = (x/x_{max})^{\alpha} if x < x_{max}, 1 otherwise$
This was about all of the mathematics that drives glove word vectors. There is a normal loss function which can be easily optimized by building neural net using tensorflow. Will add a post on my python implementation of Glove using TensorFlow too. Although the code can be viewed on Github.
